1. 序論

日本は国土の約７０パーセントを山林が占めているため、集落や構造物が山岳地帯周辺に密集している 地域が多く存在する。そのため山岳地帯付近では厳冬期には、しばしば雪崩が発生し、遭難、家屋の倒 壊などの被害をもたらすことがある。
このような雪崩の被害を未然に防止するためには、雪崩の流動機構を把握することが重要となる。 雪崩の流動シミュレーションにより流動範囲を知ることができれば、雪崩防災地域の策定を行うことが 可能となり、ハザードマップなどの種々の雪崩災害防止施設の設計に反映することもできる。

2. 研究目的

本研究は、山岳地帯にしばしば発生する煙型表層雪崩に着目し、その挙動を明らかにするための数値 シミュレーションを作成し、その妥当性の検討を行うことを目的としている。

3. 解析方法

煙型雪崩は実質的に、浮遊した雪粒子と空気の混合流体の密度と周囲の空気との密度の差による重力に よって流動する流れであり、濃度差によって生ずる密度流と類似点が多い。そのため、本研究ではモデル に傾斜サーマル理論を採用している。しかしながら、煙型雪崩では、雪崩全体の雪の量が変化するため そのままサーマル理論を利用ことは適用できない。したがって、サーマル理論を発展させた乱れエネルギー の収支までを考慮した四式モデル解析法を用いて解析を行った。
数値解析には、解析結果が計算結果の比較が容易にできるようなエクセル形式でのデータ出力を可能とし、 また、算出されたデータをビットマップ形式でのデータグラフ出力ができるプログラムを作成し、 解析を行った。

4. 解析結果

作成したプログラムを新潟県西頚城郡能生町間柵口地区権現岳で発生した表層雪崩（柵口雪崩）に適用し、 雪崩の数値解析に用いられる諸変数を変化させることによって雪崩の挙動特性が明らかにした。

5. 結論

雪粒子の特性である粒径、抵抗係数、摩擦係数や、雪崩の流動特性の解析に使われる空気の連行係数を変化 させた結果、雪崩の流動機構に関する係数の把握ができた。

我が国は大小約3000の島からなり、海岸線は34265kmにも及んでおり、国土の約70％が山岳地帯となっている。 このため、古くから低平地である沿岸平野部に人口が集中してきた。現在わが国の海岸付近は道路、鉄道などの 交通施設や人々の憩いの場として利用され､人々にとって欠かすことのできない場ではあるが、台風、 冬季波浪などの厳しい自然条件やダムによって起こる海への土砂流出の減少、海岸自体の地盤沈下、海岸への 土砂供給のアンバランスによって年々砂浜が侵食される傾向のある海岸が多い。 また、日本の海岸は種種の 海岸構造物の設置により複雑な形状をなしている｡このような複雑な現象を理解するためには数値実験や室内 実験が欠かせない。本研究ではより現実的な海岸波動場を数値実験によって表現するため、波動の分散性を 考慮した波動場数値モデルを用いて、多方向不規則波に対する波動場、海浜流、地形変化、および構造物との 相互関係を把握することを目的とする。

本研究では、二次元の修正ブシネスク方程式をと多方向不規則波を用いて波動場の数値計算を行った。 海浜流の流速は流量を水深で除し、波の1周期にわたって平均することによって計算した。流速は２次元を 仮定し、鉛直方向に平均された流れ場について計算を行った。地形変化には漂砂現象が大きく関係しており、 海浜流によって各地点ごとの漂砂量と方向を求め、地形変化の計算には底質量保存式を用いた。

本研究はモデルケースとし一様勾配を持つ海浜モデルに、構造物がない場合､潜堤(海面下1.5m)を設置した 場合､離岸堤(高さ1.5m)を設置した場合について計算を行った。モデルケースについては岸沖方向500m、 沿岸方向1000mの領域をdx=5m、dy=5mのメッシュで覆い、それぞれ100×200の領域とした。また､これらを 基礎とし、新潟西海岸の実地形を取り入れて数値計算を行った.実地形を取り入れたケースについては岸沖 方向2550m、沿岸方向2300mの領域をdx=5m、dy=5mのメッシュで覆い、それぞれ510×460の領域とした。 どちらも計算時間間隔は0.1秒とした。

本研究を行うことにより以下の知見を得るに至った。修正ブシネスク方程式により、波の分散性や波の進行 にともなう屈折、構造物による回折を計算できた。多方向不規則波を計算に取り入れることができた。 また、砕波項の空間分布より砕波帯を空間的にとらえることができた。海浜流やそれに伴う地形変化を ベイラードによって提案された漂砂量、掃流砂量およびそれに伴う地形変化の時間発展を計算できた。 室内実験と数値計算の結果との定性的な一致が得られた｡

吹雪は煙型雪崩の発生要因の一つとも考えられ，その流動特性を知ることは，固気ニ相流の基本的な 流動特性を把握するばかりでなく，雪崩の発生要因の推定という意味でも興味がある。

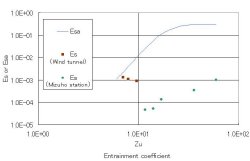
本研究の目的は，発達過程にある地吹雪について数値計算を行い，風洞実験で発生させた小スケールの 地吹雪、さらには南極みずほ基地で観測された、現地規模の吹雪との比較を行う。数値モデルとしては、 雪粒子の濃度勾配による成層効果を表現し得るモデルのうちもっとも単純なモデルであるk−ε乱流モデル を採用した。雪粒子の輸送を沈降速度を考慮した乱流拡散方程式で表されると仮定した。吹雪の特性を 表す飛雪流量の分布に着目し、実験結果・観測結果と数値モデルによる計算値と比較することにより、 モデルの妥当性を検討した。

数値解と比較したのは、科学技術庁防災科学技術研究所新庄雪氷防災研究支所の雪氷防災実験棟内にある 低温風洞装置を用いて行われた、福嶋他(2001)の風速分布、飛雪流量分布の実験結果を用いた。 現地観測として、南極みずほ基地において行われた西村(北大低温研、2001)の風速、飛雪流量の観測結果を 用いた。

風洞実験との比較において、風速分布は実験値、数値解ともに壁面から離れるにしたがって増加する、 平板上の乱流境界層の特性を再現している。飛雪流量分布は、底面直上から急速に減少し、15cmほどで 零になる。これは、雪粒子の密度が空気の密度よりはるかに大きいため、底面より離れた領域まで浮遊を 維持することが難しいためである。現地観測との比較においては、計算では無次元圧力勾配Ipを調整する ことによって、風速の大きさを調整できる。現地では高さ3mでの風速が測定されており、この値と数値解が 一致するように圧力勾配の値を調整した。この場合も風速分布は壁面流れの分布形を示すことが確認された。 飛雪流量分布との比較では、沈降速度を調整し、特に底面付近で測定値と数値解が一致するように試行錯誤 した。密度が既知の場合、沈降速度は無風時における雪粒子の力の釣り合い式から求められる。今回、 現場の測定では、SPCにより雪粒子の粒径が実測されている。そこで、飛雪流量分布の実測値と数値解の 比較から求めた沈降速度と粒径を用いて、密度を逆算した。風洞実験・現地観測との比較における今回の 雪の連行係数Esの値は、Garciaの式より2桁ほど小さく、砂の連行係数Esaよりもかなり小さい。これは、 水中での砂粒子の比重に比べて、空気に対する雪粒子の比重が極めて大きいことによると考えている。

本研究で用いた数値解析手法によって、風洞実験での小スケールの地吹雪、現地観測の大スケールの 地吹雪を説明できることを示した。また、雪の連行係数Esを算出し、その値が開水路の土砂流から得られた 値に比べて非常に小さいことが分かった。

わが国は国土の10%にあたる洪水氾濫区域（洪水時の河川水位よりも地盤の低い地域）に総人口の50%、 資産の75%が集中しているといわれ、夏季の豪雨の時期には洪水氾濫による甚大な被害を受けやすい 状況に置かれている。このため古くから堤防の建設や河川改修等によって洪水を発生させない対策が 推進されてきた。しかしながら、都市化の進展や土地利用の高度化が進み、河川改修工事による洪水 対策が困難な状況となってきた。また平成11年の福岡水害、平成12年の東海水害に代表されるように、 新たな問題として中小都市河川による都市型水害が見られるようになってきた。土地の低い市街地では 中小河川の氾濫が起りやすいだけでなく、周辺に降った雨が流れ込んでくるため堤内地の排水が追い つかずに下水溝から溢れ出すといった内水氾濫や、地下空間への浸水などの問題が発生しやすくなって いる。このため国土交通省では河川が氾濫することをある程度許容した政策に転換しつつある。

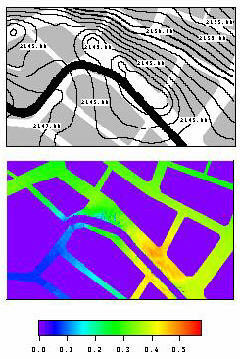
このような状況で被害を軽減するために、情報を伝達し日ごろから洪水災害に対する住民の防災意識の 涵養などソフト面の対策も重要である。このために、行政機関により氾濫シミュレーションを行ったり、 ハザードマップ（洪水氾濫区域図に避難地等の情報を表示したもの）を作成したりする動きがある。 しかし従来の氾濫のシミュレーションは格子間隔が例えば500mと広く、都市における中小河川に対して 適用することが事実上不可能である。

このような背景から、本研究ではより解像度の高いシミュレーションの開発を目的に、非線形長波 方程式を用いて氾濫を計算するアルゴリズムを作成し、仮想的に作成した地形に対して従来の氾濫計算 より細かい格子間隔で計算を行った。さらに実地形への適用として長岡市中心部を流れる柿川流域に ついて、マンホール標高データと住区データを利用して詳細な土地情報を作成し、格子間隔1mという これまでに類を見ないほどの高分解能で氾濫計算を行った。その結果より、都市域の中小河川を対象 とした氾濫シミュレーションの可能性を示すことができた。

斜面上にある固体粒子が何らかの原因で浮遊すると、重力の効果により斜面方向に流動し傾斜 サーマルを形成する。傾斜サーマルは、流下に従い渦運動を伴うため複雑な流動特性を示し、 未だ十分な解明がなされていない。従って自然現象などと密接に関わっている傾斜サーマルの 流動特性を明らかにすることは工学的に重要である。

そこで、本研究では、保存性傾斜サーマルについて実験と理論的な検討を行なう。実験では、 周囲流体に淡水を用い、流入流体にはプラスチック粒子で可視化された塩水を用いて二次元的に 傾斜サーマルを再現し、流下速度・最大厚さの測定を行う。またサーマルの内部特性として画像 解析によって流速ベクトルを求める。そして、それぞれの結果を数値解析結果と比較・検討する ことを目的とする。

二次元傾斜サーマル再現実験の実験装置は、傾斜角30°の水槽で、水路長200cm、高さ100cm、 水路幅30cmの矩形アクリル製水槽に幅15cmのアクリル板を30°に固定したものを用いた。流体の 流入方法は引き上げ式のゲートを採用し、塩水の濃度は1%、3%、5%の3種類について実験を行った。 また、このときの実験映像を記録し、その映像をもとに画像解析により流速ベクトルの算出を行なった。

傾斜サーマルの解析モデルはk-ε乱流モデル、離散化手法はSIMPLE法を用いた。基礎方程式として、 連続式，x方向運動方程式，z方向運動方程式，拡散方程式，乱流運動方程式，分子粘性逸散率を用いた。

実験値と解析値の比較で、流動特性として流下速度は、大まかな傾向は示している。実験で見られた 初期濃度が大きくなることによる流下速度のばらつきも解析結果で表れていることが分かる。最大厚さ の比較では、解析値が実験値にほぼ一致しており良い傾向の再現ができている。1%の流下距離80cm以降で 実験値が低い値となっている。これは、実験値があまり良い結果が得られなかったことと、解析結果で 流下距離80cm以降の最大厚さをmax濃度としていためである。

内部特性として流速ベクトル比較は、実験結果より傾斜サーマルは、底面付近流下方向・フロント部 巻上げ・後部巻き込み流速ベクトルの大きく3つに分かれた。これは、解析結果でもよく再現できていた。 また、最大流速ベクトルは先端部ではなく底面中央部辺りにあり、流下距離が進むにつれ徐々に 後方へと移行していることが分かった。実験により見られた流下距離が進むにつれて移り変わる、巻き上げ， 巻き込み，流下方向流速ベクトルの割合変化も、解析により特徴を捉えていた。

結論としては、流下速度は流下距離に対してほぼ一定となった。流下距離60cmまででは良好な再現結果が 得られなかった。しかし、流下距離60~120cmでは良い結果が得られ、全体としては、妥当であると考えられる。 最大厚さは流下距離に対してほぼ一次関数的に増加していることなど、数値解析でも良好な再現ができた。 流速ベクトルでは、実験により見られた底面付近流下方向・フロント部巻き上がり・後部巻き込み流速 ベクトルが数値解析でも確認することができた。また、流下距離が進むにつれ最大の流速ベクトルが 先端から中央、そして後方へと移動している様子が良好に再現できた。

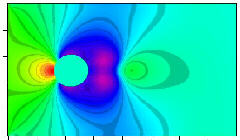
数値流体力学は近年の計算機能力の向上によってめざましく進歩しており、構造物周辺の 流れ場に対する理解も進んできている。しかしながら、これまでは、静止している円柱、 角柱などのように構造物は静止している場合を対象としていることが多かった。円や翼の ように複雑な形状の構造物を考える場合、境界の形状に適合させた境界適応格子が採用さ れている。このため物体が複雑に移動する問題では逆に取り扱いを困難にしている側面が ある。流れに影響を受けながら移動する物体運動の例としては、破提氾濫や高潮の氾濫に よって氾濫水とともに流入してくる多量の流木の挙動、空力弾性問題としてのタコマ橋の 崩壊などが考えられる。タコマ橋の崩壊は風が吹くことで橋の周りに渦ができ、その渦か らの周期的な力とタコマ橋のねじれ振動が共振を起こしてしまった渦励振であると言われ ている。このように流れにより物体が移動する場合、流体と物体の相互干渉により静止し た物体周辺の流れとはかなり異なった流れ構造が生じる。本研究では、数値的に取り扱い が容易な静止直交座標での流れ場シミュレーションと計算領域内で情報から格子空間内に 物体の形状を表現するモデルを導入し、流れ場と移動物体との相互干渉を計算できるモデ ルを作成した。比較のため1)静止している物体、2)強制的に移動、回転している物体、3) 流体力に応じて自由に移動・回転する物体の3ケースを対象として数値実験を行った。本 研究では円、楕円を流れ場に表現し、静止したものと回転させたものの比較行った。円、 楕円の静止させたものに作用する流体現象は実験により可視化で示された結果と同じよう に表現された。回転した円、楕円に作用する流体現象は円については実在の流体現象に近 い結果が得られたが、楕円に関しては流れが複雑であり、実現象の結果がなく正確に比較 は出来なかった。しかしこの円、楕円の静止している場合と強制的に移動させている場合 の数値計算の比較から物体が移動する場合、流れに与える影響は静止した場合と大きく異 なることがわかった。運動方程式の導入による物体が自由に移動する問題については物体 に作用する流れの力により移動することを表すことができた。

日本は、古くから高潮や津波などの長周期波の遡上による被害が多く、その対策も長年行われてきた。 このため高潮の長周期による人的災害はかなり軽減した。しかしながら、1999年9月24日の9918号台風では、 熊本県の不知火町において12名の犠牲者を出すなど、高潮の被災が完全になくなってしまったわけで はない。一方、津波による被害は、発生源の予測が困難であり、今後ともその危険性を回避することは 困難である。また地球温暖化による平均水位の上昇により長周期波の遡上による被災の発生の可能性が 増大している。日本の各自治体は、高潮・津波による冠水域についてのハザードマップを作成して その対策に取り組んでいる。水災害における被害を軽減し、人口、資産の集積する都市・地域における 海岸の安全性を向上させるために、波の遡上の力学的性質や地形との干渉について十分理解しておく 必要がある。従来、長周期波の遡上について、数多くの数値計算例が報告されているがそれらの多くは 沿岸の地形情報、例えば標高値の精度が十分でない場合が多く、また様々な方向から襲来することを 想定した波の入射方向の検討が不十分である。遡上を計算するには、冠水域とそうでない領域とを 判別するアルゴリズムが必要であり、また水塊が分離しても安定して計算できるスキームである必要がある。

本研究は、高潮や津波などの長周期波の遡上に関する簡便な数値波動プログラムを作成した。 さらに格子点上の地形データ（DEM）を生成する手法を開発し、新潟西港および東港を対象として地形や 海洋構造物の配置によって影響を受ける長周期波の遡上の挙動を検討したものである。

DEM（デジタル標高データモデル）の作成は、新潟港の東西21.3ｋｍ、南北15.9ｋｍの範囲を対象とした。 この範囲には700点を越す海・陸標高データが地図上に示されている。この地図をスキャナで読み込み、 該当範囲内にある海・陸の水平座標と標高値を読み取り、ファイルで保存する。この後、平面2次元上の 格子点と全海・全陸との水平距離を求め、距離の逆数に関係した重みつき平均をとって格子点上の標高とした。

平面2次元の流体運動を表す基礎方程式は非線形長波方程式であり、陽解法で離散化した式を用いて波動場の 数値計算を行う。非線形長波方程式は連続式と砕波減衰項を付加した運動方程式から成っている。 遡上計算では、水没している領域と陸上領域とが不規則に計算空間に分布している。このためこの領域を 判別するためのフラッグファイルを作成する。具体的には2次元の計算格子各点に2次元配列を対応させ、 その値が例えば1ならば水没領域、0ならば陸上あるいは引き波によって海底が露出した領域になるように 判別する。基礎方程式による計算は、冠水域と判定された領域に対してのみ行う。本研究では、新潟港に 対して計算を行った。計算領域は沿岸方向21.3kｍ、岸方向15.9kｍ、最大水深120ｍとする。全計算 時間1500秒、入射波は新潟地震の際の周期960ｓ、波高2.0ｍで入射方向は北を90度として30度間隔で 与えている。波は計算領域内、上端で発生させ、右、左、下端では反射の影響を除外した。

本研究では、波の遡上すなわち押し波時の水際の後退、また遡上していく波と引き波とによる水塊の 分離などが計算できるプログラムを作成し、実海岸に適用して様々な波向きを考慮した津波 シミュレーションを行い、沿岸域のおける遡上計算を行った。その結果、長周期波の空間的な分布特性が 地形形状に鋭敏に影響されることや新潟港の危険区域の予測を行うことができた。

密度流とは、二種類の流体の密度の差が起因となり斜面方向に流動する運動であり、自然において、 あるいは人工的に頻繁に発生する。湖や貯水池で観察される泥水流や河口部における塩水くさび、 大気における寒冷前線や海軟風、厳冬期山岳地帯で発生する煙型雪崩や火山活動に伴う火砕流などは その代表例である。

傾斜サーマルには、流下に伴い渦運動を伴うため複雑な流動形状を示し、今だ十分な解明が成されて いない。また、これらの現象は自然現象と密接に関わっており、自然災害とも関係する。したがって、 その流動特性を明らかにすることは重要である。例えば、雪崩の流動特性を把握することにより、 災害防止にも役立つこととなる。また、傾斜サーマルは密度差の原因が溶解性の塩分濃度差や温度差 などの「保存性」である場合と、固体粒子を浮遊する「非保存性」である場合に大別される。

そこで、本研究では、保存性傾斜サーマルについて実験を行い、流下特性・流動特性がどのように 変化するか実験的に調べ、理論的に検討を行う。実験においては、周囲の液体には淡水を用い、 流入流体にはプラスチック粒子を混ぜ可視化させた塩水を用いて、傾斜サーマルを再現し、 流下速度と最大厚さの測定を行う。また傾斜サーマルの内部構造を画像解析により流速ベクトルを表し、 明らかにする。

二次元的に傾斜サーマルを再現し､流下特性として最大厚さ･流下速度を、サーマルの内部特性として 流速ベクトルを求めた。流下速度については、初期濃度の増加により流下速度が増加することがわかった。 最大厚さについては、初期濃度が増加しても最大厚さの特性はあまり変化しないことがわかった。 また、流速ベクトルの測定によりサーマルは、フロント部の巻き上がり，後部の巻込み， そして底面の流下方向ベクトルと大きく3つに分かれることがわかった。また、初期濃度が大きいほうが 激しい渦運動がみられ、流下距離が進むにつれ複雑な渦運動を示した。

理論的検討としては、本実験で得られた結果を用いた保存性傾斜サーマルの数値解析を行い、 実験値と比較してその妥当性を検討した。実験値は、傾斜サーマルについての室内実験を行い その流下特性として流下速度･最大厚さの測定を行った。数値計算では、保存性傾斜サーマルに対して 連行係数αと抗力係数CDをパラメーターとして、流下速度･最大厚さの流下方向変化を求め、実験値との 比較を行った。その結果、αを0.5，CDを0.4〜0.8とすることで解析結果は実験結果を良好に再現できる ことがわかった。

社会の工業化が進み、様々な化学物質が広く一般に使用されるようになり、生体に対する撹乱を 与える化学物質が海域に放出され新たな海域環境問題として社会的関心が集まっている。 海域環境問題の実態を把握するためには数値実験が不可欠である。本研究では、海域環境問題へ の応用へ資する目的で沿岸海洋における流動・物質拡散数値モデルの作成を行った。そして潮流、 海上風、密度場などの外力の流れへの影響や水表面での熱フラックスによる密度場の変化などを 与えて計算を行い、基礎的なモデルのパフォーマンスを確認することを目的としている。

数値実験においては数値的に取り扱いが容易な直交矩形格子による計算領域の分割、基礎方程式の 離散化を行い、内湾での流動シミュレーションモデルを作成した。流体を非圧縮性流体、圧力を 静水圧近似と仮定した。この場合、２次元流動の基礎式は連続式とナビエ-ストークス方程式、 静水圧の式を用いた。その他、海水の塩素量拡散、温度の拡散、密度の変化、地形を条件として 与え、乱流モデルを適用する。乱流モデルについてはLESや 鉛直拡散係数についてリチャードソン 数により評価する方法などを適宜採用した。海上からの熱フラックスの出入りや温度と塩分から 密度を計算する方法などは文献の巻末などに掲載されている式を用いて厳密に評価した。

本数値モデルに対する境界条件としては、海上風、大気と海水面間の熱の流入出、波の入射条件、 構造物や海底面での固体壁の条件などがある。今回の数値計算は時間の制約のため長時間の計算は 行っていない。このため２番目の大気・海水面上の熱の流入出は計算の結果にはほとんど影響しない。 しかしながら長時間の計算については不可欠な条件である。計算領域は、水平方向10ｋｍ、 深さ方向約100m、時間間隔0.1秒で24800ステップの計算を行った。これは本来の目的に照らしてかなり 時間が短いが、今回は基礎的な対象に適用してモデルとしての機能を確認するに止める。 外力としては海上風および計算領域の端部から入射する長周期の波である。また、一様流体および 温度と塩分を与えて安定な２成層の密度場に対して計算を行った。

本研究による知見は、基礎的な境界形状を持つ領域に対するシミュレーションモデルの作成により、 時間経過に対する密度、流速、乱流粘性係数の分布状態を知ることができ、また、海上風、入射波、 密度分布による条件を適宜変化させて計算を行い、密度分布が一様な場合と二成層の場合で界面の 変動による流速変動を示すことができたことである。

一般に、閉鎖性海域では、湾口部付近の潮流による水平循環流と、湾奥部の海水交換性の 悪い停滞性水域が存在している。この流れの弱い停滞性水域では、富栄養な河川水や工業廃水が 流入し、長時間滞留することから水質環境の悪化が問題となっている。また、停滞性水域は、 流れが静穏なため格好の開発対象となり、さらに水質が悪化するという悪循環に陥っている。

このような閉鎖性海域の有効利用と環境保全を考える為には、海域内の流動機構と海水交換性を 明らかにし、その予測を可能にすることが重要な課題である。

そこで本研究では、代表的な閉鎖性水域である広島湾を例に、湾内の流れと海水交換に関する 3次元数値シミュレーションを行い、湾内水の流動機構を把握する事を試みた。 本研究では、流れの3次元多層モデルを用いて、基礎方程式を陽的に差分し、潮汐流の数値 シミュレーションをおこなった。

対象領域は、広島湾（南北約50ｋｍ、東西約30ｋｍの楕円形湾）とし、計算格子間隔は、 600ｍ×600ｍとした。また、水深を鉛直方向に11層に分割し、1〜6層を5ｍ、7〜10層を10ｍ、 11層を20ｍの厚さとし、3次元数値シミュレーションを行った。

計算では、始めに、広島湾において潮流が安定するまでの周期を求め、シミュレーション 実行周期を決定した。

次に、広島湾内の水位変動を求めた。この結果の再現性を確かめるため、観測値と比較した。 また、湾内全体の水位変動の等深線図を描き、広島湾の水位変動特性も調べた。

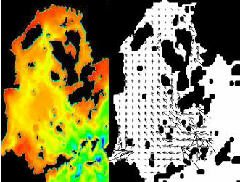
次に、広島湾内1、3、5層の流速を求めた。この結果も、観測値と比較することにより 再現性を確かめた。また、湾全体の潮流ベクトル図、等速線図を描くことにより、湾内の 流況状態も調べた。湾内の潮汐流の最大流速は、湾口付近で30ｃｍ/ｓ程度、湾奥部で3ｃｍ/ｓ 程度である事が分かった。また、計算値と観測値の流速は、非常によく一致したため、 広島湾の潮汐流をよく再現できたことが分かり、湾内の流動機構を把握する手法として、 3次元数値シミュレーションの有効性を確認した。

次に、広島湾の長期間の流況特性を調べるため、潮汐残差流の検討を行った。これも、 潮汐流と同様に、1、3、5層についての潮汐残差流の流速を求めた。また、ベクトル図を描き、 潮汐残差流の流況特性も調べた。これについても、再現性を確かめるために、観測結果と比較した。 また潮汐残差流の流速は、湾口付近で0.7ｃｍ/ｓ、湾央付近で0.2ｃｍ/ｓ、湾奥付近で0.7ｃｍ/ｓ 程度である事が分かった。この流速は、微小であり、広島湾の海水交換性は非常に悪く、 海水は滞留しやすい事が分かった。

海水から発生する飛沫・飛来塩分は、沿岸域の住民の生活に影響を与えるばかりでなく、コンクリート 構造物の耐久性を悪化させる主要因であり、その動態を把握することが強く望まれている。飛来塩分の 実体は、未だ未解明の部分が多く、たとえば、飛沫(水滴)に解けこんでいる成分やエアロゾルとして 沿岸から数キロ程度飛来するものもある。本研究では、波のエネルギーが砕波によって気泡の発生に 寄与し、その結果、飛来塩分が発生するというモデルを構築し、数値実験を実施した。また、発生した 飛来塩分は、風に乗って拡散する計算もあわせて行い、陸域の輸送も計算した。

砕波から発生する飛来塩分には、大きく２つに大別することができる。�@砕波によって海水面が ちぎれることによって発生する飛沫、�A砕波によって生成される気泡から発生する飛沫である。 本研究では、内陸部の塩害に非常に強く関係する粋表面の気泡(�A)によって発生する飛沫について 計算を行った。以下にその内容について説明する。飛来塩分の発生要因となる海水面下の気泡は、 砕波によって海水面が乱れることで生成される。この気泡は、海水表面で破裂すると同時に飛沫を 発生させる。そのため、本計算モデルでは、海水面の乱れの度合いをエネルギー減衰量とし、海水面下に 生成される気泡量および気泡から発生する飛沫量を計算することによって、飛来塩分の発生量の計算を行った。

本研究では、従来あまり検討されてこなかった砕波からの飛沫の発生に関する数値計算モデルの開発および 検討を行った。その結果、本計算モデルは、砕波から発生する飛沫を十分に計算できることが明らかになった。 また、本研究により、飛来塩分の発生から輸送までを表した計算モデルが開発された。その結果、 潜堤を用いることで飛来塩分の内陸部への輸送量を軽減できることが明らかになった。