環境・建設計算機実習Ⅱ
目 次
1.目的
潮汐の1次元非定常の流れの計算をおこなうことにより、非定常での差分数値計算方法を修得する。
2.水の流れ
場所:自然:川、海、地下水など
室内:実験など
現象:定常・非定常、等流・不等流など
解析:1次元、2次元、3次元
3.実習の手順
4.流れの方程式(式の導出)
流れの方程式は次の2式で連立される。
①運動方程式(ニュートンの第二法則)
②連続方程式(質量保存則)
本章では、2方程式の導出をおこなう。
4.1 質点系と流体系の運動表記法の相違
(1) Euler的方法
簡単のためにx方向の運動のみを考える。質点の運動は、ニュートン力学の第2法則により次式で表される。
ここに、t:時間、X(t):時間tにおける質点のx座標、m:質点の質量、Fx:x方向の外力、x方向の質点の速度は速度はVx=dX/dtであるから、上式は
とも書ける。
ところで、流れの流体粒子は(波などの周期運動の場合を除けば)遥か遠方からやって来て、また遥か彼方へと去ってしまうし、また流体粒子には特別な標識がついて区別し得るわけではないから,個々の流体粒子の位置X(t)を問題にするのは不便である。それゆえ、水理学や流体力学では流体場のそれぞれの場所での速度を問題とし、これを従属変数すなわち未知量とする。
したがって、流れを取り扱う場合には、計測が容易である点からも実際上の知りたい量であることかrも、そしてたてられた基礎方程式の解き易さからも、空間の固定点でも各瞬間の流速を問題とする。この場合、流体粒子のの各方向の速度成分は、点の座標(x,y,z)と時間tを独立変数としてそれぞれ
u(x,y,z,t), v(x,y,z,t), w(x,y,z,t)
と表される。このような取り扱い方法、われわれはEuler的手法という。なお、いちいちu=f1(x,y,z,t)などと書く代わりに単にu(x,y,z,t)と書く。
質点系の運動では個々の質点の位置と速度を問題とするが、水理学の場合にこれと同様に一つ一つの流体粒子を追跡して、その速度に関して理論を展開する方法をLagrange的手法という。しかし上述の理由からこの方法は、波の運動、地下水の初期運動、拡散などの特別な場合にも応用されることがあるくらいで、それもこの方法でなければならないというものではない。
なお、Euler的方法(Eulerの運動方程式)もLagrange的方法(Lagrangeの運動方程式も共により導かれたもではあるが、Lagrangeが後者の方法を多用したことにより2つの方法はこのように呼び分けられている。
(2) 流れ場の未知量
質点系の場合とは異なり、流れの状態の未知量は流速成分u,v,wの他に、流体の内部応力ともいうべき圧力pも未知量である。
P(x,y,z,t)
圧力とは流体中の任意の面に垂直にこれに向かう方向に働く応力である。応力とは単位面積あたりに働く力をいう。
流体中の考えている面に沿う方向に働く応力を剪断応力という。剪断応力は粘性を有する流体の相対的なずり運動により発生する。この応力もまた内部応力で未知量であるが、これは流速の空間変化率により表されるので従属変数ではない。また、対象によっては、密度、濃度、温度などが未知量となる場合があるが、その場合にはこれらに関する方程式が新たに付け加わる。最も単純化されしかも実用上十分な問題設定が、流速成分u,v,wと圧力pを未知量とするもである。
空気などの気体では流体の圧縮性を考慮しなければならない場合がある。この場合には密度ρも従属変数であり、このような流体は圧縮流体といわれる。水理学で対象とする水の流れは普通密度が一定の非圧縮性流体として取り扱ってよい。水の流れで圧縮性が問題となるのは管路を伝わる水撃圧の問題などである。
(3) 加速度の表記法
質点の場合のx方向の加速度はαx=dvx/dtであるが、Euler的方法における流体の加速度は単純にはこうはならない。それは、流体粒子は刻々位置を変えているのに、Euler的方法の速度とは固定された一点での速度にすぎないからである。
数学的にみれば、vx=uはtの他にx,y,z,にも関連し、加速度をtに関する微分のみで表現しなければならないということである。
表
- 1 質点と流体との速度・加速度表示の相違|
|
質点 |
流体 |
|
位置 |
X(t) |
- |
|
速度 |
|
u(x,y,z,t) |
|
加速度 |
|
|
例えば、 のように徐々に狭くなる管の流れを考えると、定常な流れでは一点Pでの速度
upは一定で図
- 1 移流加速度(一点での速度は不変でも、流体粒子の加速度は0とは限らない。)
4.2 運動方程式
未知量を求めるにはその未知量の数だけの方程式が必要である。これが以下に述べるx,y,zの3方向の運動方程式(あるいは運動量方程式)を質量の保存を表す連続の方程式の合計4つの方程式である。この4つをまとめて運動方程式と呼ぶこともあり、それと区別するために、前の3つの方程式をその表す意味により運動量方程式とよぶこともある。
(1) 連続の方程式
連続の方程式は流体運動における質量保存則である。流体中の一点P
を中心にx,y,z方向の一辺がδx,δy,δzの直方体の部分を考える。ここに出入りする微小時間δtあたりの流体の質量を考える。
まず、x軸に垂直な2つの面で考える。
左方からの流入量:ρu(x,y,z,t)δyδzδt
右方からの流出量:ρu(x+δx,y,z,t)δyδzδt
したがって、左右の2つの面からの流出量は差し引き次のようになる。
x軸方向の流出量:
同様に、y軸、z軸方向の2つの面からの流出流入量の差から
y軸方向の流出量:
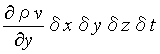
z軸方向の流出量:
これらの和が直方体δxδyδz内の質量の増加
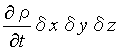
であるので、
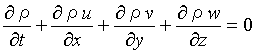
の関係が成立する。
ここで、非圧縮性流体では
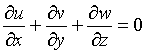
である。
(2) Eulerの運動方程式
ニュートンの運動の第2法則は、力をF、加速度を、質量をmとすると
F=mα
と書かれる。すでに述べたように、流体粒子には固体や質点系のように決まった目印がないから、このままでは流体運動に適用できない。
(a) 加速度
そこで流体の1点P(x,y,z)に着目すると、この点の流速は(u,v,w)で、Δt時間後には点Q(x',y',z')へ移動する。x'=x+Δx, y'=y+Δy, z'=z+Δzはそれぞれ、点Pでの流速u,v,wで点Qに移動した結果と考えられるので、
Δ
x=u(x,y,z)ΔtΔ
y=v(x,y,z)ΔtΔ
z=w(x,y,z)Δtと書ける。
この時点(t+Δt)での点Q(x',y',z')の流速はu,v,wをΔx,Δy,Δz,Δtに関してTaylor展開し、微小量の二次以上の項を省略すれば
u(x',y',z',t')=u(x+Δx,y+Δy,z+Δz,t+Δt)
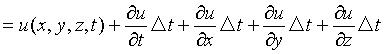
と書ける。
さらに、上式の関係を代入すれば、
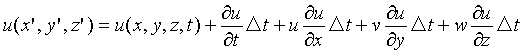
したがって、x方向へのこの流体粒子の加速度は、Δt→0として、
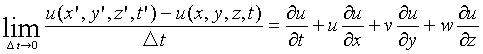
となる。これをDu/Dtと表す。
y方向とz方向に関する加速度も同様に導かれる。これらをまとめると、
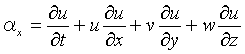
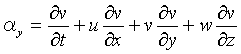
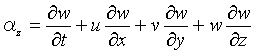
(b) 力
一方、直方体の流体粒子に作用する力は、単位質量あたりにF=(Fx,Fy,Fz)
の外力と非粘性流体(完全流体)の場合には直方体の各面に働く圧力pである。x軸に垂直な2つの面の圧力は互いに方向が逆でその大きさは
左の面: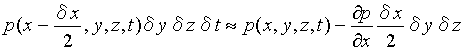
右の面: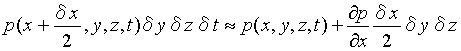
である。
したがって、左右両面の圧力差は
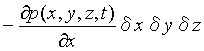
である。
同様にy軸およびz軸に垂直な2面の圧力差はそれぞれ
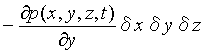 、
、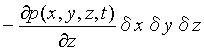
となる。
(c)Eulerの方程式
したがって、x軸方向の運動方程式は
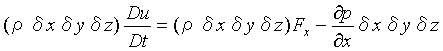
すなわち
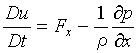
である。同様な式がy軸、z軸方向についても得られ、これらを並べると運動方程式は次のようになる。
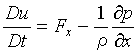 、
、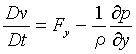 、
、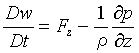
より具体的に書けば、完全流体についてのEulerの運動方程式は次式となる。
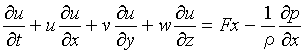
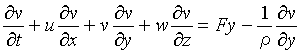

(d) Navier-Stokesの方程式
実在の粘性流体では、運動方程式に粘性による剪断応力の項を加えなければならず、その項(ν∇2uなど)を加えたものがその式となる。
5.実習で使用する方程式
本実習では数値計算の初期段階なので、単純化した1次元の運動方程式と連続式を使用する。
式は次式で表される。
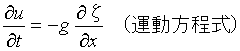
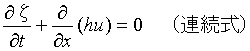
6.差分式
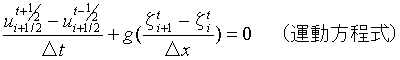
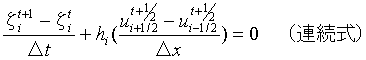
7.計算条件
計算方法
(1)強制水位
i=1で水位を与え、時間を発展させて計算をおこなう。
水位はζ=Asin(ωt)=Asin[(2π/T)k(Δt/2)] (k=0,1.2....)
(2)格子間隔および格子数
Δx=1000m、100格子とする。(1000m×100格子=100km)
(3)地形および水深
地形は、片側を開境界、もう片方を閉境界とする。
水深は次の2とおりを計算する。
①全域で20mとする。
②開境界側半分(50格子)を50m、閉境界側半分(50格子)を20m
(4)周期
日本の太平洋付近では月の引力によって発生する潮汐が卓越しているので、この流れを仮想する。よってT=12hとする。
(5)計算時間(タイム・ステップ)
タイム・ステップは計算の安定性、収束性を支配するもので、一般に、次の関係を満足しなければならない。
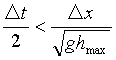
8.課題
次の各課題について水深が全域で20mの場合と、50m,20mの場合について計算をしなさい。
①外境界付近および中央部、閉境界付近の3ケ所における水位と流速の時間変化の図を出力しなさい。
②外境界で入力された波が閉境界側(湾奥部)に伝わって行く様子を各自工夫して出力しなさい。
9.提出について
(1)図面の出力形式は自由とする(ex.EXCEL)。ただし教官にわかるように出力のこと。
(2)提出日は12月24日までとし、教官室まで直接持参のこと。
(3)不明な点があったら直ちに質問すること。
E-mail: inu@nagaokaut.ac.jp
℡9624GLESCO
( GLobe, EStuary and COast )
Hydrauric Engineering Lab. Nagaoka University of Technology